1. 基于支持向量机(SVM)的回归-SVR

Support Vector Regression(SVR)
已知：
$$y = wx + b$$
求 W,b -- 使得回归的线性函数对两侧的支持向量有最小间距

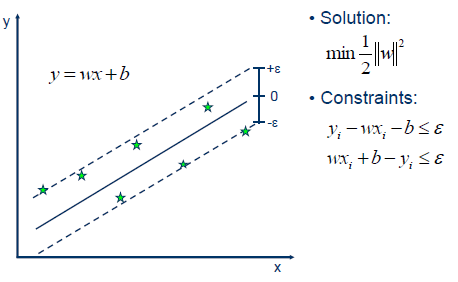
1.1. SVR

svr=SVR(
    C=1.0, 
    cache_size=200,
    coef0=0.0, 
    degree=3, 
    epsilon=0.1,
    gamma=`auto_deprecated`, 
    kernel=`rbf`,
    max_iter=-1, 
    shrinking=True,
    tol=0.001, 
    verbose=False
    )

参数说明
-epsilon 距离误差

1.2. LinearSVR

LinearSVR(
    C=1.0, 
    dual=True, 
    epsilon=0.0, 
    fit_intercept=True,
    intercept_scaling=1.0, loss=`epsilon_insensitive`, max_iter=1000,
    random_state=None, 
    tol=0.0001, 
    verbose=0)

内核岭回归L2

sklearn.kernel_ridge.KernelRidge(
    alpha=1, 
    kernel=`linear`, 
    gamma=None, 
    degree=3, 
    coef0=1, 
    kernel_params=None)

参数解释
1. alpha:
2. kernel : string or callable, default=”linear”
Kernel mapping used internally. A callable should accept two arguments and the keyword arguments passed to this object as kernel_params, and should return a floating point number.
3. gamma : float, default=None
- rbf、laplacian、多项式、指数chi2和sigmoid核的gamma参数。
4. degree : float, default=3
- 只针对polynomial kernel核有效，对于其他核忽略
5. coef0 : float, default=1
Zero coefficient for polynomial and sigmoid kernels. Ignored by other kernels.

内核岭回归（KRR）将岭回归（具有L2-范数正则化的线性最小二乘）与核技巧结合在一起。

KRR学习的模型的形式与支持向量回归（SVR）相同。但是，使用了不同的损失函数：KRR使用平方误差损失，而支持向量回归使用epsilon不敏感损失，两者均与12正则化结合。

与SVR相比，KRR模型的拟合可以封闭形式进行，对于中等规模的数据集通常更快。另一方面，学习的模型是非稀疏的，因此比SVR慢，后者在预测时学习epsilon> 0的稀疏模型。

2. 线性回归

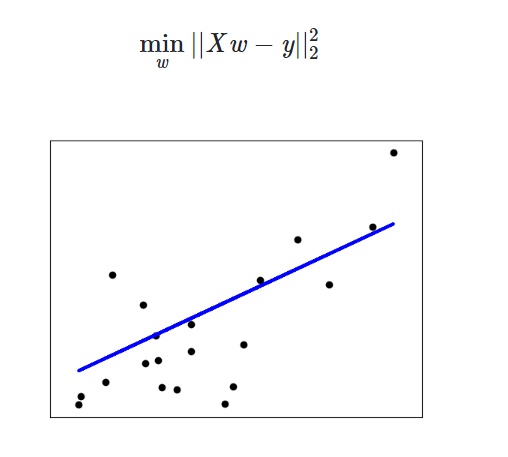
对于:
$$y^{hat}=wX+b$$
求W，b, Loss function = MSE
$$min L(y_i,y^{hat})=L(y_i,Wx+b)$$

2.1. 普通线性回归

linear_model.LinearRegression 使用普通小二乘法OLS的线性回归

$$ Loss=(y - wX)^2 $$

$$ w=(X^TX)^{-1}X^Ty $$

权重w只与输入数据(x,y)相关，要求 X 不为全0。

sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)
# fit_intercept 拟合截距
# copy_X 在X.copy上操作

参数说明

fit_intercept[defualt=True] 拟合截距
copy_X[defualt=True]在X.copy上操作

2.2. 岭回归 L2

$$ Loss=(y - Xw)^2 + alpha \times w^2$$

sklearn.linear_model.Ridge(
    alpha=1.0, 
    fit_intercept=True,
    normalize=False, 
    copy_X=True, 
    max_iter=None, 
    tol=0.001, 
    solver=`auto`,
    random_state=None)

参数解释
- solver [defualt="auto"]
- auto:根据数据类型自动选择求解器
- svd :奇异值分解SVD Singular Value Decomposition
- cholesky: 使用标准的 scipy.linalg.solve 函数获得一个封闭解
- sparse_cg: 使用scipy.sparse.linalg.cg中的共轭梯度解算器作为一种迭代算法，这个解算器比cholesky更适合于大规模数据（设置tol和max_iter的可能性）。
- lsqr: 使用 scipy.sparse.linalg.lsqr 求解，最快的迭代方法
- sag: 使用随机平均梯度下降
- saga: 使用其无偏版本随机平均梯度下降
- max_iter 共轭梯度求解器的最大迭代次数
- sparse_cg和lsqr求解器，默认值由scipy.sparse.linalg确定
- sag求解器，默认值为1000

linear_model.Ridge 岭回归，一种将L2作为正则化工具的线性小二乘回归
linear_model.RidgeCV 带交叉验证的岭回归
linear_model.RidgeClassiﬁer 岭回归的分类器
linear_model.RidgeClassiﬁerCV 带交叉验证的岭回归的分类器
linear_model.ridge_regression 【函数】用正太方程法求解岭回归

2.4. LASSO回归 L1

$$Loss=\frac{1}{2 * n} * (y - Xw)^2 + alpha * |w|$$
在sklearn中，lasso回归使用的就是坐标下降法

sklearn.linear_model.Lasso(
    alpha=1.0, 
    fit_intercept=True,
    normalize=False, 
    precompute=False,
    copy_X=True, 
    max_iter=1000,
    tol=0.0001, 
    warm_start=False, 
    positive=False, 
    random_state=None, 
    selection=`cyclic`)

参数解释
1. precompute:
- 是否使用预先计算的 Gram 矩阵来加速计算。
2. tol
- 数据解算精度。
3. positive
- positive: 强制系数为正值。

selection[defualt=cyclic]:
- cyclic: 循环每次迭代使用原来的seed
- random: 每次迭代都会更新一个seed。设置random 通常会使得收敛更加迅速，特别是设置tol>1e-4。

linear_model.Lasso Lasso，使用L1作为正则化工具来训练的线性回归模型
linear_model.LassoCV 带交叉验证和正则化迭代路径的Lasso
linear_model.LassoLars 使用小角度回归求解的Lasso
linear_model.LassoLarsCV 带交叉验证的使用小角度回归求解的Lasso
linear_model.LassoLarsIC
使用BIC或AIC进行模型选择的，使用小角度回归求解的 Lasso
linear_model.MultiTaskLasso 使用L1 / L2混合范数作为正则化工具训练的多标签Lasso
linear_model.MultiTaskLassoCV
使用L1 / L2混合范数作为正则化工具训练的，带交叉验证的多标签Lasso
linear_model.lasso_path 【函数】用坐标下降计算Lasso路径

2.5. ElasticNet 弹性网回归 L1+L2

β=(λI+K)−1yβ=(λI+K)−1y

$$ Loss=\frac{1}{2n}(y-Xw)^2+alpha \times l1 \times ratio|w|+ \frac{alpha}{2}(1 - l1 \times ratio) w^2$$

sklearn.linear_model.ElasticNet(
    alpha=1.0, 
    l1_ratio=0.5, 
    fit_intercept=True, 
    normalize=False, 
    precompute=False,
    max_iter=1000, 
    copy_X=True, 
    tol=0.0001, 
    warm_start=False, 
    positive=False, 
    random_state=None, 
    selection=`cyclic`)

linear_model.ElasticNet 弹性网，一种将L1和L2组合作为正则化工具的线性回归
linear_model.ElasticNetCV 带交叉验证和正则化迭代路径的弹性网
linear_model.MultiTaskElasticNet 多标签弹性网
linear_model.MultiTaskElasticNetCV 带交叉验证的多标签弹性网
linear_model.enet_path 【函数】用坐标下降法计算弹性网的路径